세그먼트 트리
- = Segment Tree = Statisitc Tree
- 간격이 있는 숫자나 세그먼트에 대한 데이터를 저장하는데 사용하는 트리 구조
- 여러 데이터가 연속적으로 존재할 때, 특정 범위의 데이터 합을 구할 때 유용하다.
배열에 데이터가 아래와 같이 있다고 가정해보자.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 5 | 6 | 2 | 3 | 4 | 3 | 5 | 2 | 1 |
위 배열에서 인덱스 1부터 5까지의 합을 구하려면?
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 5 | 6 | 2 | 3 | 4 | 3 | 5 | 2 | 1 |
위 범위의 데이터를 하나씩 더하는 방식을 사용하면 된다. (=선형적)
데이터가 N개면 시간복잡도가 O(N)이 된다.
이를 개선하기 위해서 세그먼트 트리를 이용한다면 시간복잡도를 줄일 수 있다.
위의 배열을 아래와 같이 트리 구조로 생각해보자.
(파란 글씨는 index, 원 안의 숫자는 value)
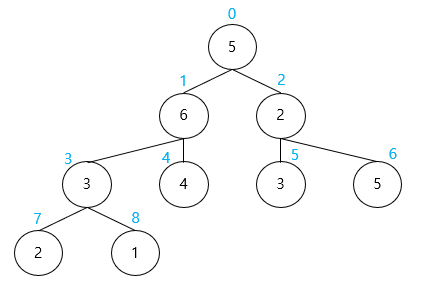
데이터의 합을 저장하는 트리 구조를 새로 생성한다. (이 포스팅에서는 구간 합 트리라고 부르겠다.)
최상단에는 데이터의 전체 합을 넣고, 왼쪽 노드, 오른쪽 노드에 각각 반절의 합을 넣는다.
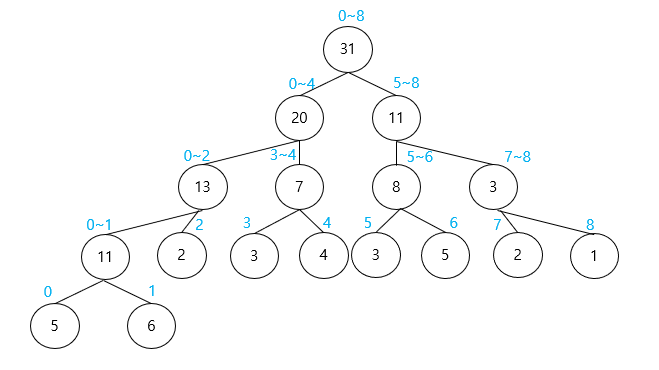
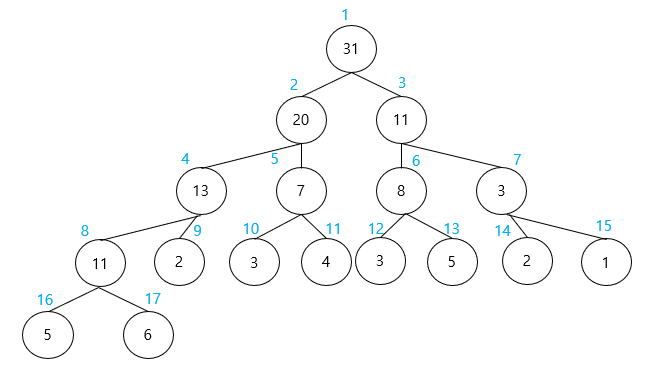
위를 배열 형태로 살펴보면 아래와 같다.
구간 합 트리의 경우 2를 곱했을 때 왼쪽 자식 노드를 가리키기 위해 index를 1부터 사용한다.
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| value | 31 | 20 | 11 | 13 | 7 | 8 | 3 | 11 | 2 | 3 | 4 | 3 | 5 | 2 | 1 | 5 | 6 | |
여기서 주목해야할 점은 본래 배열의 개수는 9개였는데, 구간 합 트리의 개수는 18개가 되었다.
구간 합 트리는 최소한 본래 배열의 2*n의 공간이 필요하다.
위 트리를 생성하는 코드는 아래와 같다.
/* 부분 합 트리 생성
* start: arr의 시작 index
* end: arr의 끝 index
* node: sumTree의 현재 노드 index
*/
int init(int start, int end, int node) {
if(start == end) return sumTree[node] = arr[start];
int mid = (start + end) / 2;
return sumTree[node] = init(start, mid, node*2) + init(mid+1, end, node*2+1);
}🔻 코드 설명
1. start == end
위의 경우, node는 sumTree의 리프 노드의 인덱스를 의미한다.
해당 노드들은 arr의 특정 구간의 합이 아닌 특정 인덱스 값을 넣게 된다.
2. 좌측 노드와 우측 노드에 범위를 나눌 mid를 구한다. (start와 end의 중간값)
3. 현재 노드에 좌측 노드와 우측 노드의 합을 넣는다.
좌측 노드와 우측 노드를 구하기 위해 각각 init메소드를 재귀적으로 실행시키게 된다.
위와 같은 구간 합은 트리 구조로 인해 생성 시간이 O(logN)이 걸린다.
탐색도 마찬가지로 O(logN)이 걸리는데 예시를 한번 살펴보자.
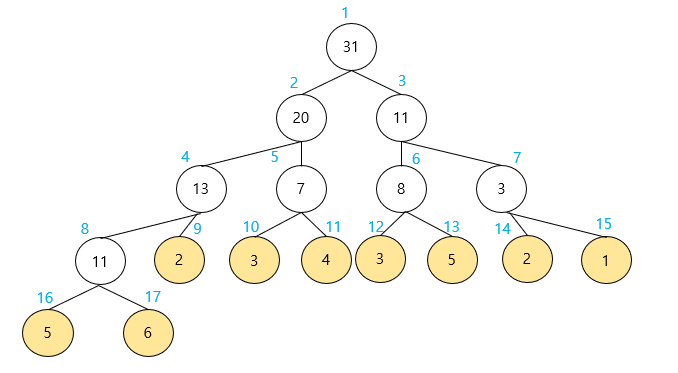
인덱스 3부터 6까지의 합을 구하려고 할때, 구간 합 트리에서 아래 노드에 대한 정보만 알면 된다.
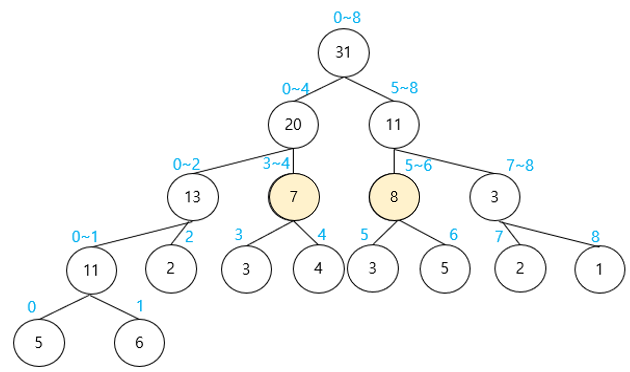
인덱스 범위에 해당하는 부분에 대해서만 합하면 되니 구하기 쉬워진다.
/* 부분 합 트리 - 특정 구간 합
* start: arr의 시작 index
* end: arr의 끝 index
* node: sumTree의 현재 노드 index
* left: 합을 구하려는 구간의 왼쪽 index
* right: 합을 구하려는 구간의 오른쪽 index
*/
int sum(int start, int end, int node, int left, int right) {
if(start > right && end < left) return 0; // 범위 밖
if(start >= left && end <= right) return sumTree[node]; // 범위 내
int mid = (start + end) / 2;
return sum(start, mid, node*2, left, right)
+ sum(mid+1, end, node*2+1, left, right);
}
특정 원소 값을 수정하려면 해당 값이 포함된 노드만 수정하면 된다.
만약 arr의 3번 인덱스를 수정하고 싶다면, 수정할 노드는 아래와 같다.
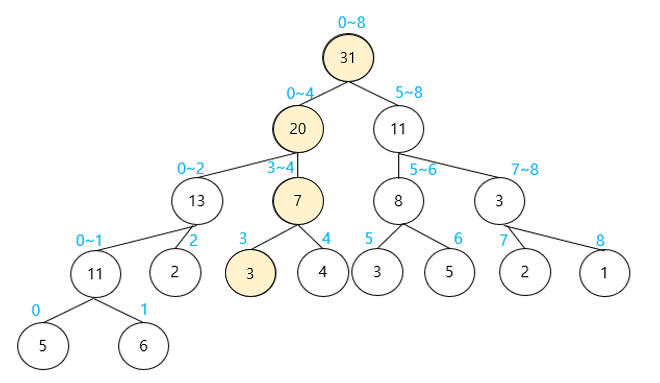
/* 부분 합 트리 - 특정 노드 수정
* start: 시작 index
* end: 끝 index
* node: sumTree 현재 노드의 index
* index: arr의 수정하려는 index
* value: arr의 수정하려는 값 - arr의 원래 값
*/
void updateNode (int start, int end, int node, int index, int value) {
if(start > index || end < index) return; // 범위 밖
sumTree[node] += value;
if(start == end) return;
int mid = (start + end) / 2;
updateNode(start, mid, node*2, index, value);
updateNode(mid+1, end, node*2+1, index, value);
}참고
- 세그먼트 트리: https://en.wikipedia.org/wiki/Segment_tree
- 특정 범위의 데이터 합: https://m.blog.naver.com/ndb796/221282210534
'Develop > etc' 카테고리의 다른 글
| Entity vs DTO vs VO (3) | 2021.11.23 |
|---|---|
| [GitHub] Pull Request와 코드리뷰 (0) | 2021.11.11 |
| 최적화 문제 - 완전 탐색, 동적 프로그래밍, 탐욕적 방법 (0) | 2021.10.03 |
| [Log4j] no service named is available 에러 (1) | 2021.07.21 |
| 템플릿, 프레임워크, 라이브러리, API의 차이 (0) | 2021.07.01 |


