목차
1. 최적화 문제
2. 완전 탐색
3. 동적 프로그래밍
3-1. 행렬 경로
3-2. 최장 공통 부분순서; LCS
3-3. 최장 증가 부분수열; LIS
4. 탐욕적 방법
4-1. 연속 배낭문제
4-2. 스케줄 짜기 문제
시작하기 앞서..
해당 포스팅은 최적화 문제를 해결하는 방법 중, '완전 탐색, 동적 프로그래밍, 탐욕적 방법'에 대해 다룬다.
각 유형에 해당하는 몇 가지 문제를 예제로 보이며 언어는 Java를 이용한다.
대학생 때 공부한 것을 정리하는 차원에서 포스팅 하는거라 입문자에게는 어려운 내용일 수 있다😅
최적화 문제; Optimization problem
- 문제에 대한 하나 이상의 후보 해답이 존재하고, 각 후보 해답은 최적임을 판단할 근거가 되는 값을 가질 때, 이 들 중 최적값을 구하너가 최적 값에 해당하는 후보 해답을 구하는 문제
- 흔히 완전 탐색, 동적 프로그래밍, 탐욕적 방법 3가지로 풀 수 있다.
- ex: 최단 경로 문제, 배낭 채우기 문제, ...
완전 탐색; brute-force search
- 모든 경우의 수를 탐색해 최적화 구하기
- 모든 경우의 수를 탐색하기 때문에 오래 걸린다.
동적 프로그래밍; dynamic-programming
- 작은 문제를 먼저 해결하고 이 결과를 저장해 더 큰 문제의 해결에 반복적으로 적용
- 상향식 접근 방법 (bottom-up)
🔻 동적 프로그래밍과 유사한 '분할 정복'
분할 정복 알고리즘
- 문제를 부분 문제로 분할 -> 부분 문제들을 재귀적으로 해결 -> 이 결과들을 결합해 원래의 문제 해결
- 하향식 접근 방법 (top-down)
- 부분 문제들이 서로 독립적인 문제로 분할될 때 유용.
예제를 통해 차이점을 비교해보자.
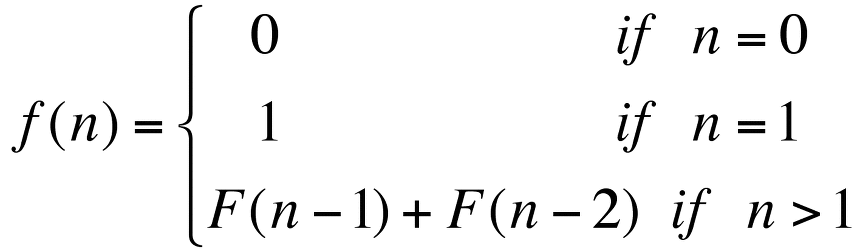
분할 정복으로 구현한 피보나치
public static int fibo(int n) {
if (n==0 || n==1) return n;
return fibo(n-1) + fibo(n-2);
}코드 예제를 통해 문제를 부분 문제로 분할한다는 것이 얼핏 이해가 갈 것이다.
- fibo(n)을 fibo(n-1) + fibo(n-2)로 분할하고,
- fibo(n-1)과 fibo(n-2)를 각각 구한 뒤,
- fibo(n-1)과 fibo(n-2)의 결과들을 결합해 fibo(n)을 구한다.
하지만 이 경우에는 O(2^n)이라는 시간 복잡도가 지수 시간으로 발생해버린다.
동적 프로그래밍으로 구현한 피보나치
public static int fibo(int n) {
int[] arr = new int[n+1];
arr[0] = 0; arr[1] = 1;
for(int i=2;i<n+1;i++) {
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n];
}- f(0), f(1), ... 등의 작은 문제를 먼저 해결하고
- 이 결과를 arr라는 배열에 저장해
- 더 큰 문제의 해결에 반복적으로 사용하고 있다.
이 경우에는 n+1만큼의 배열을 저장할 공간이 필요하지만 시간 복잡도 면에서는 O(n)의 시간이 소요된다.
문제 유형 살펴보기
1. 행렬 경로
n*n 행렬의 (0,0)에서 (n,n) 위치까지로 이동하는데 이동 경로상의 점수 합이 최대로 하는 경로 찾는 문제
(단, 오른쪽 또는 아래쪽으로만 이동이 가능하다.)
행렬 m [][]
| 6 | 7 | 12 | 5 |
| 5 | 3 | 11 | 18 |
| 7 | 17 | 3 | 3 |
| 8 | 10 | 14 | 9 |
🔻 코드
public static int getBestRoute() {
int[][] arr = {{6,7,12,5},{5,3,11,18},{7,17,3,3},{8,10,14,9}};
int n = arr.length;
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
if(i==0 && j==0) {
continue;
} else if (i==0) {
arr[i][j] += arr[i][j-1];
} else if (j==0) {
arr[i][j] += arr[i-1][j];
} else {
arr[i][j] += Math.max(arr[i][j-1], arr[i-1][j]);
}
}
}
return arr[n-1][n-1];
}
2. 최장 공통 부분순서
= LCS; Longest Common Subsequence
두 문자열에서 공통적으로 나타나는 부분 순서들 중에서 가장 긴 것의 글자 수 구하기
ex: "abcba"와 "abdb"의 LCS는 "abb"이 되고 문제의 정답은 3. (순서를 유지하며 공통되는 문자를 뽑아냄)
코딩테스트 (백준): https://www.acmicpc.net/problem/9251
🔻 코드
public static int getResult(String s1, String s2) {
String[] s1Arr = s1.split("");
String[] s2Arr = s2.split("");
int x = s1Arr.length + 1;
int y = s2Arr.length + 1;
int[][] arr = new int[x][y];
for(int i=1;i<x;i++) {
for(int j=1;j<y;j++) {
if(s1Arr[i-1].equals(s2Arr[j-1])) {
arr[i][j] = arr[i-1][j-1] + 1;
} else {
arr[i][j] = Math.max(arr[i-1][j], arr[i][j-1]);
}
}
} return arr[x-1][y-1];
}
코드를 설명하자면 아래 테이블을 참고하면 된다.
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| A | P | P | L | E | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | P | 0 | 0 | 1 | 1 | 1 | 1 |
| 2 | A | 0 | 1 | 1 | 1 | 1 | 1 |
| 3 | P | 0 | 1 | 2 | 2 | 2 | 2 |
| 4 | E | 0 | 1 | 2 | 2 | 2 | 3 |
| 5 | R | 0 | 1 | 2 | 2 | 2 | 3 |
숫자가 1씩 커진 부분을 살펴보면 A, P, E가 된다.
(1,2)를 1로 기준 두고 P, P, E라고 보아도 된다.
(5,5) 위치를 보면 LCS의 길이인 3을 구할 수 있는 것이 보인다.
그 외 사용 예제
- Bioinformanmatics: DNS 시퀀스의 염기서열 비교를 통한 유사성 판정
- 유닉스 diff utility: 라인 기반의 파일 비교 유틸리티
- Screen redisplay in "emacs": 터미널에 가능한 적은 숫자의 문자를 업데이트
- Reviesion controle system
- 편집거리(edit distance) 문제
편집거리란? 어떤 문자열을 다른 문자열로 변환하는데 필요한 최소 연산의 수
3. 최장 증가 부분수열
= LIIS; Longest Increasing Subsequence
n개의 수로 이루어진 수열에서 가장 긴 증가 부분 수열 찾기
코딩 테스트 (백준): https://www.acmicpc.net/workbook/view/801
🔻 코드
int getResult(int[] numArr, int n) { // numArr: 수열, n: 수열에 들어있는 숫자 개수
int[] cntArr = new int[n];
int max = 0;
for(int i=0;i<n;i++) {
int cnt = 1;
for(int j=0;j<i;j++) {
if(numArr[i] == numArr[j]) {
cnt = cntArr[j];
} else if (numArr[i] > numArr[j] && cnt <= cntArr[j]){
cnt = cntArr[j] + 1;
}
}
cntArr[i] = cnt;
max = Math.max(max, cnt);
}
return max;
}수열의 모든 요소에 대해 for문을 돌며
(0 ... 현재 인덱스-1)까지의 요소를 이용해 cnt를 찾는다.
그 외 사용 예제
- 상자 넣기 문제
- 꼬인 전깃줄 절선 문제
🔻 그 외 사용 예제 추가 설명
* 상자 넣기 문제
상자 크기가 1, 6, 2, 4, 7, 3, 5, 6 순서대로 주어진다고 가정하자.
이 때 최대한 많은 상자를 사용한다고 할때 몇 개를 사용할 수 있는가?
-> 1, 2, 4, 5, 6을 사용해 총 5개
* 꼬인 전깃줄 절선 문제
전깃줄이 아래와 같이 꼬여있다고 가정할 때, 꼬이지 않기 위해 잘라야하는 선 수는?
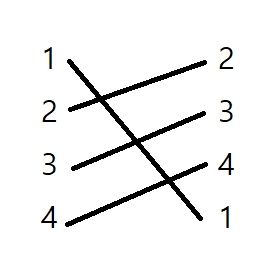
-> 1을 자르면 된다. 총 1개.
탐욕적 방법
- 공집합에서 시작해, 탐욕적 기준에 따라 최선의 아이템을 차례로 추가해 문제의 사례에 대한 해답이 될 때까지 곗혹하는 기법
- 동적 계획법에 비해 개발이 쉽지만, 항상 최적해를 보장하지 않으므로 증명이 필요
문제 유형 살펴보기
1. 연속 배낭 문제
아이템이 n개에 각자 가치가 존재할 때, 용량을 초과하지 않으면서 배낭에 담는 아이템의 가치가 최대가 되도록 담기. (단, 아이템은 잘라서 담을 수 있다.)
🔻 코드
연속 배낭 문제의 경우, 가중치 순으로 정렬만 하면 되니 코드를 생략한다.
🔻 배낭 문제의 동적 프로그래밍과 탐욕적 방법
배낭 문제에 대해서는 두 가지 유형이 있다.
- 아이템을 자를 수 없는 Knapsack Problem
- 아이템을 자를 수 있는 Fractional Knapsack Problem
2의 경우에는 가장 높은 가치를 가진 아이템부터 넣다가 용량이 초과되는 경우 아이템을 자르면 된다.
높은 가치 순으로 정렬만 하면 되니 O(nlogn)의 시간복잡도가 걸린다.
다만 1의 경우에는 아이템을 자를 수 없어서 구하는 방법도 달라진다.
동적 프로그래밍 방법으로 접근해서 풀어볼 것!
쪼갤 수 없는 배낭에 대해서는 백준 12865번을 풀어보면 된다.
2. 스케줄 짜기 문제
-1. 각 작업에 걸리는 시간이 주어졌을 때, 대기 시간을 포함해 모든 작업을 완료하는데 걸리는 시간이 최소가 되도록 스케쥴 짜기
-2. 각 작업에는 이익과 마감시간이 할당되어 있을 때, 최대한의 이익을 얻도록 스케줄 짜기 (Deadline Scheduling)
코테 (백준): https://www.acmicpc.net/problem/1781
🔻 코드
public class Main {
public static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
// 1. input
int n = Integer.parseInt(bf.readLine());
List<Problem> list = new ArrayList<Problem>();
for(int i=0;i<n;i++) {
list.add(new Problem(i, bf.readLine()));
}
// 2. sort - 정렬 기준: 마감기한
Collections.sort(list);
// 3. select problem
PriorityQueue<Integer> q = new PriorityQueue<>();
for(Problem p: list) {
q.add(p.cnt);
if(q.size() > p.deadline) {
q.poll();
}
}
// 4. calculate
int answer = 0;
while(!q.isEmpty()) {
answer += q.poll();
}
// 5. print
bw.write(answer+"\n");
bf.close();
bw.close();
}
}
class Problem implements Comparable<Problem> {
int num;
int deadline;
int cnt;
Problem(int num, String str) {
this.num = num;
String[] arr = str.split(" ");
this.deadline = Integer.parseInt(arr[0]);
this.cnt = Integer.parseInt(arr[1]);
}
@Override
public int compareTo(Problem p) {
return this.deadline - p.deadline;
}
}마감 기한 기준으로 정렬 후 PriorityQueue를 이용한다.
PriorityQueue에는 아이템의 가치 (cnt)를 넣는데, 만약 PriorityQueue에 넣은 개수가 작업 시간보다 클 경우 PriorityQueue의 요소를 하나 제거한다.
PriorityQueue를 poll()하는 경우, 가장 작은 값이 제거된다.
'Develop > etc' 카테고리의 다른 글
| [GitHub] Pull Request와 코드리뷰 (0) | 2021.11.11 |
|---|---|
| 세그먼트 트리 개념과 구현 (0) | 2021.10.22 |
| [Log4j] no service named is available 에러 (1) | 2021.07.21 |
| 템플릿, 프레임워크, 라이브러리, API의 차이 (0) | 2021.07.01 |
| [Eclipse] 프로젝트 세팅 시 오류 목록 (0) | 2021.06.01 |


